了解 DSA 中的中缀、后缀和前缀表达式/符号
数学表达式通常涉及复杂的运算,读者或计算机需要根据操作的优先级来理解这些表达式。表达式可以通过不同的表示法来表示,每种表示法都有其相对的优缺点。本文将讨论三种流行的表达法:中缀、前缀和后缀。
一、中缀表达式
中缀表达式是操作符位于操作数之间的数学表达式。这是人类最常用的数学表示法。例如,表达式 5 + 7 是一个中缀表达式。在这个表达式中,操作符 + 位于操作数 5 和 7 之间。尽管这种表示法对人类而言直观易懂,但对于计算机来说,计算结果的效率可能受到影响,因为必须遵循操作的优先级,而括号又会改变默认优先级。
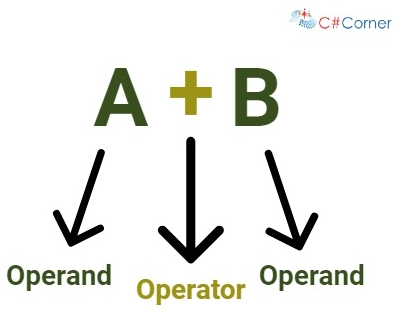
1.1 中缀表达式的书写方式
-
中缀表示法是人们最熟悉的表示法。例如, A + B是中缀表示法。 -
操作数位于操作符两侧,在表达式 A + B中,加法操作符+位于操作数A和B之间。 -
操作的优先级通过括号来指定,例如, (A + B) * C强制要求在乘法之前进行加法。
1.2 操作符优先级规则
中缀表达式中,每个操作符都有与之相关的优先级规则,这些规则指定了在表达式中评估操作符的顺序。乘法和除法的优先级高于加法和减法。因此,在表达式 A + B * C 中,乘法操作将在加法之前进行。
| 操作符 | 优先级 |
|---|---|
| 括号 () | 最高 |
| 指数 ^ | 高 |
| 乘法 * | 中等 |
| 除法 / | 中等 |
| 加法 + | 低 |
| 减法 - | 低 |
1.3 评估中缀表达式
评估中缀表达式需要额外的处理来管理操作顺序和括号。首先,将中缀表达式转换为后缀表达式。这可以通过使用栈或递归算法实现,然后对后缀表达式进行评估。
中缀表达式的优缺点
-
优点:
-
对人类来说更自然、更易读和理解。 -
广泛使用,受大多数编程语言和计算器的支持。
-
-
缺点:
-
需要括号来指定操作顺序。 -
解析和高效评估可能比较困难。
-
二、前缀表达式(波兰表示法)
前缀表达式,也称为波兰表示法,是一种数学表示法,其中操作符位于操作数之前。这与中缀表示法不同,后者将操作符放在操作数之间。在前缀表示法中,操作符首先被写出,后面跟着其操作数。例如,中缀表达式 A + B 在前缀表示法中将写为 + A B。
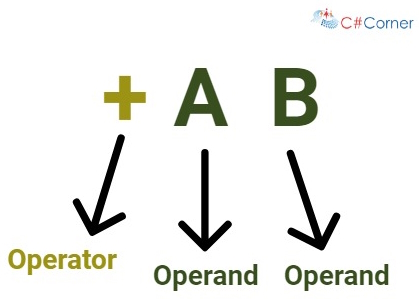
2.1 评估前缀表达式
前缀表达式在处理许多嵌套括号的表达式或使用基于栈的编程语言时非常有用。
前缀表达式的优缺点
-
优点:
-
不需要括号,因为操作符总是位于操作数之前。 -
使用基于栈的算法进行解析和评估更容易。 -
在涉及许多嵌套括号的表达式中更高效。
-
-
缺点:
-
对人类来说较难阅读和理解。 -
使用较少,普及程度低于中缀表示法。
-
2.2 前缀表达式的示例代码
#include <iostream>
#include <stack>
#include <cmath>
using namespace std;
// 评估前缀表达式的函数
int evaluatePrefixExpression(const string &expression) {
stack<int> st; // 创建一个栈用于存储操作数
// 从右到左遍历表达式
for (int i = expression.length() - 1; i >= 0; i--) {
if (isdigit(expression[i])) { // 如果是数字
st.push(expression[i] - '0'); // 将数字压入栈中
} else {
// 检查栈中是否有足够的操作数
if (st.size() < 2) {
cerr << "Error: Not enough operands for operation." << endl; // 输出错误信息
return 0;
}
int op1 = st.top(); st.pop(); // 获取第一个操作数
int op2 = st.top(); st.pop(); // 获取第二个操作数
// 根据操作符执行相应的操作
switch (expression[i]) {
case '+':
st.push(op1 + op2); // 加法
break;
case '-':
st.push(op1 - op2); // 减法
break;
case '*':
st.push(op1 * op2); // 乘法
break;
case '/':
if (op2 != 0)
st.push(op1 / op2); // 除法
else {
cerr << "Error: Division by zero." << endl; // 输出除零错误
return 0;
}
break;
case '^':
st.push(pow(op1, op2)); // 指数
break;
default:
cerr << "Error: Invalid operator encountered." << endl; // 输出无效操作符错误
return 0;
}
}
}
return st.top(); // 返回计算结果
}
int main() {
string expression = "*+45+20"; // 示例前缀表达式
cout << "The result of the prefix expression is: "
<< evaluatePrefixExpression(expression) << endl; // 输出结果
return 0;
}
// 输出 - 前缀表达式的结果是: 18
三、后缀表达式(逆波兰表示法)
后缀表达式,也称为逆波兰表示法(RPN),是一种数学表示法,其中操作符位于操作数之后。这与中缀表示法不同,后者将操作符放在操作数之间。在后缀表示法中,操作数首先被写出,后面跟着操作符。例如,中缀表达式 A + B 在后缀表示法中将写为 A B +。我们可以从左到右评估后缀表达式,每当遇到操作符时,就将其应用于先前的操作数。

3.1 评估后缀表达式
后缀表达式在涉及许多嵌套括号的情况或在使用基于栈的编程语言时非常有用。
后缀表达式的优缺点
-
优点:
-
消除了对括号的需求。 -
对人类来说更易读和理解。 -
使用频率高于前缀表示法。
-
-
缺点:
-
需要基于栈的算法进行评估。 -
在某些情况下可能比前缀表示法效率低。
-
3.2 后缀表达式的示例代码
#include <iostream>
#include <stack>
#include <cmath>
using namespace std;
// 评估后缀表达式的函数
int evaluatePostfixExpression(string str) {
stack<int> st; // 创建一个栈用于存储操作数
// 从左到右遍历表达式
for (int i = 0; i < str.length(); i++) {
if (str[i] >= '0' && str[i] <= '9') { // 如果是数字
st.push(str[i] - '0'); // 将数字压入栈中
} else {
int op2 = st.top(); // 获取第二个操作数
st.pop(); // 弹出操作数
int op1 = st.top(); // 获取第一个操作数
st.pop(); // 弹出操作数
// 根据操作符执行相应的操作
switch (str[i]) {
case '+':
st.push(op1 + op2); // 加法
break;
case '-':
st.push(op1 - op2); // 减法
break;
case '*':
st.push(op1 * op2); // 乘法
break;
case '/':
st.push(op1 / op2); // 除法
break;
case '^':
st.push(pow(op1, op2)); // 指数
break
;
default:
cout << "Invalid operator: " << str[i] << endl; // 输出无效操作符错误
return 0;
}
}
}
return st.top(); // 返回计算结果
}
int main() {
string str = "7425/+7*"; // 示例后缀表达式
int result = evaluatePostfixExpression(str); // 评估后缀表达式
cout << "The result of the postfix expression is = " << result << endl; // 输出结果
return 0;
}
// 输出 - 后缀表达式的结果是 = 28
四、中缀、前缀和后缀表达式的区别
中缀、前缀和后缀表达式之间的关键区别如下:
| 方面 | 中缀表示法 | 前缀表示法(波兰表示法) | 后缀表示法(逆波兰表示法) |
|---|---|---|---|
| 可读性 | 易于人类理解 | 不太易于人类阅读,需要熟悉 | 不太易于人类阅读,需要熟悉 |
| 操作符位置 | 在操作数之间 | 在操作数之前 | 在操作数之后 |
| 括号需求 | 经常需要 | 不需要 | 不需要 |
| 优先级处理 | 通过括号跟踪 | 固定优先级 | 固定优先级 |
| 评估方法 | 从左到右评估 | 从右到左评估 | 从左到右评估 |
| 歧义处理 | 可能需要显式括号 | 歧义很少,评估直接 | 歧义很少,评估直接 |
| 一元操作符处理 | 复杂的位置 | 由于显式符号简化 | 由于显式符号简化 |
| 计算机效率 | 由于优先级和括号不太高效 | 由于固定优先级更高效 | 由于固定优先级更高效 |
| 用法 | 广泛用于数学 | 在计算机科学和编程中常见 | 在计算机科学和编程中常见 |
五、结论
中缀、前缀和后缀表达式是表达式的三种书写和评估方式。虽然人类在阅读和书写中缀表达式时感到非常自然和直观,但在计算问题上,使用前缀或后缀表示法书写表达式对于开发用于表达式操作的计算机程序是非常有效和有用的。由于我们可以轻松地使用栈数据结构评估后缀表达式,因此后缀表达式适合于某些算法的实现。