层归一化在深度神经网络中的应用与作用

一、层归一化的数学公式

层归一化（Layer Normalization）是一种用于规范化神经网络中每一层激活值的技术。与批归一化（Batch Normalization）不同，层归一化是在每个输入的特征维度上进行归一化，这使得它在批量大小较小或变化的场景下特别有效，比如自然语言处理（NLP）模型处理可变长度序列时。

1.1 数学公式

对于给定的输入向量 (x = [x_1, x_2, ..., x_n])，层归一化计算每个神经元激活的均值 (\mu) 和方差 (\sigma^2)：

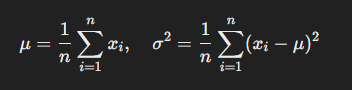
每个神经元的归一化输出为：

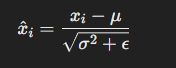
其中 (\epsilon) 是一个小常数，用于数值稳定性。接着，使用可学习的参数 (\gamma)（缩放）和 (\beta)（平移）对归一化后的值进行调整：

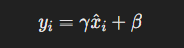
这种方法使模型能够在训练过程中保持激活值的表达能力，同时稳定分布。

二、对梯度流动和训练稳定性的影响

在深层网络中，梯度流动可能会受到消失或爆炸梯度问题的影响。通过对每层的激活进行标准化，层归一化帮助在反向传播过程中保持梯度在合理范围内。例如，在训练复杂任务如语言建模的深度前馈网络时，没有归一化的情况下，较深层的输出可能产生高度变化的梯度，导致梯度不稳定。

2.1 在变换器架构中的作用

在变换器架构中（如BERT、GPT和AlbertAGPT），层归一化在每个子层操作后进行，确保梯度不会在层之间变化过大。例如，AlbertAGPT在每个变换器块的前馈和自注意力机制之后应用层归一化。通过在每个阶段标准化输出，AlbertAGPT能够有效地平衡每层的贡献，确保模型的学习动态不会被单层的不稳定性过度影响。

三、内部协变量偏移的减少与学习效率的提高

层归一化解决了内部协变量偏移的问题，即网络参数更新时层输入分布的变化。这种偏移迫使模型不断适应新的数据分布，从而减慢训练过程。例如，在循环神经网络（RNN）中，层归一化可以显著减少协变量偏移，稳定学习过程。

3.1 在递归神经网络中的应用

在处理时间序列时，RNN的隐藏状态可以随时间变化而表现出高方差。没有归一化的情况下，学习长期依赖关系可能变得复杂。层归一化通过稳定每个时间步的输出，确保模型在处理复杂输入序列时保持稳定的学习率，从而提高训练效率。

四、深层网络中的错误积累问题

随着信息在深层网络中流动，小错误可能会累积，导致模型输出的显著偏差。层归一化缓解了这一问题。例如，在用于图像识别的深度卷积网络中，归一化帮助管理不同输入图像导致的特征激活变化。

4.1 在卷积神经网络中的作用

卷积层从输入数据中提取空间特征层次。没有归一化的情况下，较深层的激活可能过度增长，导致梯度不稳定。层归一化通过保持各层激活的一致性，减少了错误积累的可能性，从而保持了模型学习复杂、多尺度特征的能力。

五、在变换器模型中的应用

在变换器架构（如BERT、GPT和AlbertAGPT）中，层归一化在每个子层操作后起着关键作用。公式如下：

[ \text{Output} = \text{LayerNorm}(\text{Input} + \text{SubLayer}(\text{Input})) ]

这种设置有助于稳定自注意力机制的训练，因为激活的动态范围可能会显著变化。在AlbertAGPT中，层归一化确保即使在参数空间较小的情况下，模型也不会因为过度激进的学习率或不稳定的梯度幅度而不稳定。

六、管理层间的信息流动

层归一化能够保持一致的激活规模，这直接影响到信息在层间的流动。在深层网络中，由于层操作和激活函数的内在差异，层输出的尺度可能会有很大变化。例如，在使用变换器的NLP模型中，嵌入层的输出需要适当地缩放，以适应后续的注意力层。层归一化确保这些激活保持在有利于稳定训练的范围内。

6.1 在AlbertAGPT中的效果

在AlbertAGPT中，层归一化提供的连贯性确保模型可以准确地将学习到的特征从一层传递到另一层，而不会失真。这种一致性对于构建能够捕捉数据中长期依赖关系的分层表示至关重要。

七、减少对超参数的敏感性

层归一化还减少了对学习率、权重初始化和批量大小等超参数的敏感性。这种鲁棒性在处理大模型时特别有价值。例如，在没有归一化的传统训练场景中，学习率的微小变化可能会导致收敛行为的剧烈变化。层归一化通过标准化层激活，使得超参数选择更为宽松和不那么关键。

7.1 实验结果

在AlbertAGPT等模型中，层归一化使得训练可以在更广泛的学习率范围内顺利进行，减少了深度学习中通常需要的试错过程。这种灵活性对于优化模型效率尤为重要，特别是在大规模设置中。

八、增强的泛化能力和正则化效果

层归一化具有隐式的正则化效果，可以增强神经网络的泛化能力。通过保持一致的激活分布，层归一化有助于防止过拟合，这在具有高容量的深度网络中尤为重要。例如，在基于变换器的语言模型中，层归一化有助于约束模型的学习能力，使其趋向于更鲁棒的解决方案。

8.1 研究结果

实证研究表明，使用层归一化的模型在未见数据上的表现通常优于没有使用归一化的模型，这突显了其作为正则化技术的作用。在AlbertAGPT中，这使得模型在训练期间不仅能有效学习，还能在推理时保持性能。

九、与其他归一化技术的比较

虽然层归一化与批归一化（BatchNorm）在概念上有些相似，但它特别适用于批量级统计难以计算或不相关的场景。批归一化通过计算整个批次的统计量来归一化激活，使其在序列任务中效果较差。例如，在处理可变长度序列的RNN中，批归一化可能会干扰时间依赖关系，而层归一化则在批次维度上独立操作。

9.1 在AlbertAGPT中的适用性

由于输入的序列性和可变性，AlbertAGPT中层归一化的独立性允许在没有依赖批量统计的情况下进行更可靠的训练。这种独立性有助于在资源有限的设置中进行更稳定的训练。

十、层归一化研究的未来方向

关于归一化技术的持续研究探讨了将层归一化与其他方法（如组归一化和实例归一化）结合，以进一步提高训练稳定性。新方法正在开发，以动态调整缩放和移动参数，实现响应变化训练条件的自适应归一化。这些进展可能进一步提升AlbertAGPT等大规模模型的性能。

随着神经架构复杂性的不断增长，层归一化的基本原理将对保持训练效率和稳定性至关重要。未来的模型可能会利用自适应层归一化技术，在稳定性和灵活性之间优化平衡，开启人工智能研究的新前沿。

十一、结论

层归一化是一个强大的工具，通过管理梯度流动、减少内部协变量偏移和防止层间错误积累，来稳定深度神经网络的训练。在像AlbertAGPT这样的高级

架构中，它起着至关重要的作用，确保了稳定的学习动态，使其成为深度学习不断发展的领域中不可或缺的技术。