递归是一种基本的编程概念,其中一个函数通过在其自身内部调用自己来解决问题。这种方法将复杂的问题分解成更小、更易于管理的子问题。
递归的组成部分
正如我们之前讨论的那样,递归是一种函数自我调用的技术。为了理解递归,需要了解其关键组件。以下是递归的主要组成部分:
基本情形(Base Case)
基本情形是递归中的一个基础概念,它作为一个条件,决定了递归函数何时停止调用自己。这对于防止无限递归和随后的堆栈溢出错误至关重要。
基本情形提供了对最简单问题实例的直接解决方案,确保每次递归调用都向终止条件靠近一步。
计算阶乘是最常见的递归例子之一。数学上,阶乘定义如下:
n! = n × (n-1)!
可以看出,我们用阶乘本身来定义阶乘。因此,这是一个编写递归函数的好例子。让我们展开上述定义来计算5的阶乘值。
5! = 5 × 4! = 5 × 4 × 3! = 5 × 4 × 3 × 2! = 5 × 4 × 3 × 2 × 1! = 5 × 4 × 3 × 2 × 1 = 120
虽然我们可以使用循环来执行这个计算,但其递归函数涉及到成功递减该数字直到达到1。
示例
以下示例展示了如何使用递归函数来计算阶乘:
def factorial(n):
if n == 1:
print(n)
return 1
else:
print(n, '*', end=' ')
return n * factorial(n-1)
print('5的阶乘=', factorial(5))
上述程序生成了以下输出:
5 * 4 * 3 * 2 * 1
5的阶乘= 120
递归情形(Recursive Case)
递归情形是递归函数的一部分,其中函数调用自身来解决较小或更简单的问题实例。这种机制使得复杂的问题可以被分解成更易于管理的子问题,每一个都是原始问题的一个较小版本。
递归情形对于朝着基本情形进展是必要的,确保递归最终会终止。
示例
下面是一个递归情形的例子。在这个例子中,我们生成斐波那契数列,在其中递归情形是对前两个斐波那契数的结果进行求和:
def fibonacci(n):
if n <= 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
fib_series = [fibonacci(i) for i in range(6)]
print(fib_series)
上述程序生成了以下输出:
[0, 1, 1, 2, 3, 5]
使用递归的二分查找
二分查找是一种强大的算法,用于快速在排序列表中查找元素,具有对数的时间复杂度,使其非常高效。
让我们看看另一个例子来理解递归是如何工作的。当前的任务是检查一个给定的数字是否在列表中。
虽然我们可以使用一个for循环遍历列表中的每一个数字并与指定的数字比较来进行顺序搜索,但是顺序搜索效率不高,特别是在列表非常大的时候。二分查找算法检查索引'high'是否大于索引'low'。根据'mid'变量的值,函数再次被调用来搜索该元素。
我们有一个按升序排列的数字列表。找到列表的中点,并根据所希望的数字是小于还是大于中点位置的数字来限制左侧或右侧的检查范围。
下面的图显示了二分查找的工作原理:
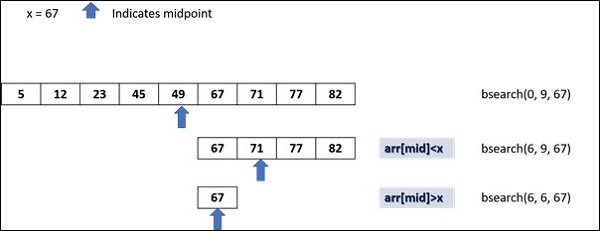
示例
以下代码实现了递归的二分查找技术:
def bsearch(my_list, low, high, elem):
if high >= low:
mid = (high + low) // 2
if my_list[mid] == elem:
return mid
elif my_list[mid] > elem:
return bsearch(my_list, low, mid - 1, elem)
else:
return bsearch(my_list, mid + 1, high, elem)
else:
return -1
my_list = [5, 12, 23, 45, 49, 67, 71, 77, 82]
num = 67
print("列表是")
print(my_list)
print("检查数字:", num)
my_result = bsearch(my_list, 0, len(my_list) - 1, num)
if my_result != -1:
print("元素在索引位置", str(my_result))
else:
print("未找到元素!")
输出:
列表是
[5, 12, 23, 45, 49, 67, 71, 77, 82]
检查数字: 67
元素在索引位置 5