神经网络是一种并行计算设备,试图建立一种计算机模型来模拟大脑的功能。主要目标是开发一个比传统系统更快执行各种计算任务的系统。这些任务包括模式识别与分类、逼近、优化和数据聚类等。
什么是人工神经网络(ANN)
人工神经网络(ANN)是一个高效的计算系统,其核心思想是从生物神经网络的类比中借鉴来的。ANN 也被称为人工神经系、并行分布式处理系统或联结主义系统。ANN 包含大量的单元,它们以某种模式相互连接,允许它们之间进行通信。这些单元,也被称作节点或神经元,是简单的并行处理器。
每一个神经元通过连接链与其他神经元相连。每个连接链都有一个权重,这个权重包含了输入信号的信息。这对神经元解决特定问题来说是最有用的信息,因为权重通常会激发或抑制正在传递的信号。每个神经元都有一个内部状态,这被称为激活信号。输出信号是在结合输入信号和激活规则后产生的,可能会发送给其他单元。
如果您想详细了解神经网络,请参考链接 —— 人工神经网络。
安装有用的软件包
为了在 Python 中创建神经网络,我们可以使用一个强大的神经网络软件包叫做 NeuroLab。这是一个包含基本神经网络算法的库,具有灵活的网络配置和学习算法。您可以使用以下命令在命令提示符下安装此软件包:
pip install NeuroLab
如果您使用的是 Anaconda 环境,则可以使用以下命令安装 NeuroLab:
conda install -c labfabulous neurolab
构建神经网络
在本节中,让我们通过使用 NeuroLab 软件包在 Python 中构建一些神经网络。
基于感知器的分类器
感知器是 ANN 的构建块。如果您想了解更多关于感知器的信息,请参考链接 —— artificial_neural_network。
下面是使用 Python 代码构建基于感知器的简单神经网络分类器的逐步执行:
导入必要的包
import matplotlib.pyplot as plt
import neurolab as nl
输入值
请注意,这是一个监督学习的例子,因此您也需要提供目标值。
input = [[0, 0], [0, 1], [1, 0], [1, 1]]
target = [[0], [0], [0], [1]]
创建网络
net = nl.net.newp([[0, 1], [0, 1]], 1)
训练网络
在这里,我们使用 Delta 规则来进行训练。
error_progress = net.train(input, target, epochs=100, show=10, lr=0.1)
可视化输出并绘制图表
plt.figure()
plt.plot(error_progress)
plt.xlabel('Number of epochs')
plt.ylabel('Training error')
plt.grid()
plt.show()
您可以看到以下图表显示了使用误差度量的训练进度:
基于感知器的分类器
单层神经网络
在这个例子中,我们将创建一个单层神经网络,该网络由独立的神经元组成,它们作用于输入数据以产生输出。请注意,我们使用的输入文件名为 neural_simple.txt。
导入有用的包
import numpy as np
import matplotlib.pyplot as plt
import neurolab as nl
加载数据集
input_data = np.loadtxt('/Users/admin/neural_simple.txt')
以下是我们将要使用的数据。请注意,在此数据中,前两列为特征,最后两列为标签。
array([[2. , 4. , 0. , 0. ],
[1.5, 3.9, 0. , 0. ],
[2.2, 4.1, 0. , 0. ],
[1.9, 4.7, 0. , 0. ],
[5.4, 2.2, 0. , 1. ],
[4.3, 7.1, 0. , 1. ],
[5.8, 4.9, 0. , 1. ],
[6.5, 3.2, 0. , 1. ],
[3. , 2. , 1. , 0. ],
[2.5, 0.5, 1. , 0. ],
[3.5, 2.1, 1. , 0. ],
[2.9, 0.3, 1. , 0. ],
[6.5, 8.3, 1. , 1. ],
[3.2, 6.2, 1. , 1. ],
[4.9, 7.8, 1. , 1. ],
[2.1, 4.8, 1. , 1. ]])
将四列分成两列的数据和两列的标签
data = input_data[:, 0:2]
labels = input_data[:, 2:]
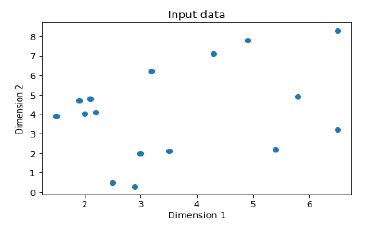
使用以下命令绘制输入数据
plt.figure()
plt.scatter(data[:,0], data[:,1])
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.title('Input data')
定义每个维度的最小值和最大值
dim1_min, dim1_max = data[:,0].min(), data[:,0].max()
dim2_min, dim2_max = data[:,1].min(), data[:,1].max()
定义输出层中的神经元数量
nn_output_layer = labels.shape[1]
定义单层神经网络
dim1 = [dim1_min, dim1_max]
dim2 = [dim2_min, dim2_max]
neural_net = nl.net.newp([dim1, dim2], nn_output_layer)
训练神经网络
error = neural_net.train(data, labels, epochs = 200, show = 20, lr = 0.01)
使用以下命令可视化和绘制训练进度
plt.figure()
plt.plot(error)
plt.xlabel('Number of epochs')
plt.ylabel('Training error')
plt.title('Training error progress')
plt.grid()
plt.show()
在上述分类器中使用测试数据点
print('\nTest Results:')
data_test = [[1.5, 3.2], [3.6, 1.7], [3.6, 5.7], [1.6, 3.9]]
for item in data_test:
print(item, '-->', neural_net.sim([item])[0])
您会发现测试结果如下:
[1.5, 3.2] --> [1. 0.]
[3.6, 1.7] --> [1. 0.]
[3.6, 5.7] --> [1. 1.]
[1.6, 3.9] --> [1. 0.]
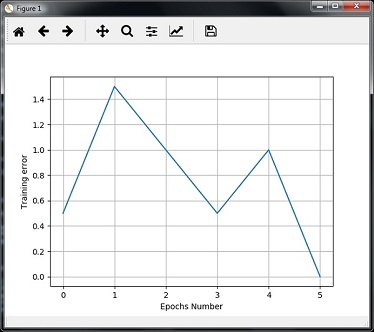
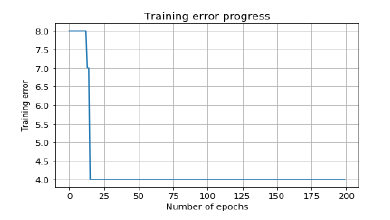
您可以看到以下图表作为上述讨论代码的输出:
单层神经网络
迭代次数
多层神经网络
在本例中,我们将创建一个多层神经网络,该网络由多于一层的结构组成,以提取训练数据中的潜在模式。这个多层神经网络将像回归器一样工作。我们将根据方程 y = 2x^2 + 8 生成一些数据点。
导入必要的包
import numpy as np
import matplotlib.pyplot as plt
import neurolab as nl
根据上述方程生成一些数据点
min_val = -30
max_val = 30
num_points = 160
x = np.linspace(min_val, max_val, num_points)
y = 2 * np.square(x) + 8
y /= np.linalg.norm(y)
重塑此数据集
data = x.reshape(num_points, 1)
labels = y.reshape(num_points, 1)
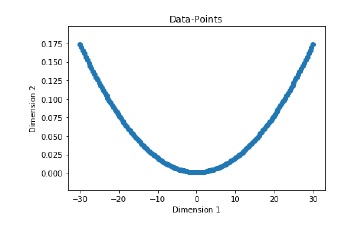
使用以下命令可视化和绘制输入数据集
plt.figure()
plt.scatter(data, labels)
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.title('Data-points')
使用 neurolab 构建具有两个隐藏层的神经网络
neural_net = nl.net.newff([[min_val, max_val]], [10, 6, 1])
现在使用梯度训练算法
neural_net.trainf = nl.train.train_gd
现在训练网络,以在上述生成的数据上学习为目标
error = neural_net.train(data, labels, epochs = 1000, show = 100, goal = 0.01)
在训练数据点上运行神经网络
output = neural_net.sim(data)
y_pred = output.reshape(num_points)
现在绘图和可视化任务
plt.figure()
plt.plot(error)
plt.xlabel('Number of epochs')
plt.ylabel('Error')
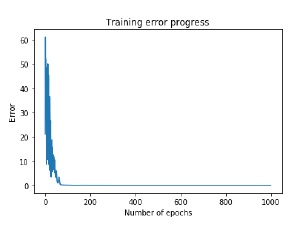
plt.title('Training error progress')
接下来我们将绘制实际输出与预测输出的对比
x_dense = np.linspace(min_val, max_val, num_points * 2)
y_dense_pred = neural_net.sim(x_dense.reshape(x_dense.size,1)).reshape(x_dense.size)
plt.figure()
plt.plot(x_dense, y_dense_pred, '-', x, y, '.', x, y_pred, 'p')
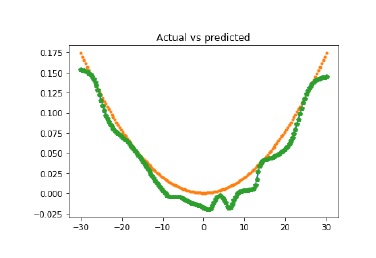
plt.title('Actual vs predicted')
plt.show()
由于上述命令的结果,您可以观察到下面所示的图表:
多层神经网络
训练误差进展
实际与预测