Python 人工智能无监督学习：聚类

非监督机器学习算法没有任何提供指导的监督者。这就是为什么它们与所谓的真正的智能紧密相关。

在非监督学习中，不会有正确的答案也没有老师来指导。算法需要自己发现数据中的有趣模式。

什么是聚类？

基本上，聚类是一种无监督学习的方法，也是统计数据分析中常用的技术，在许多领域都有应用。聚类主要是把一组观察结果划分成子集，称为簇，使得同一簇内的观察结果在一个意义上是相似的，而与其他簇中的观察结果是不同的。简单来说，聚类的主要目标是基于相似性和不相似性来对数据进行分组。

例如，下图展示了不同簇中的相似类型的数据。

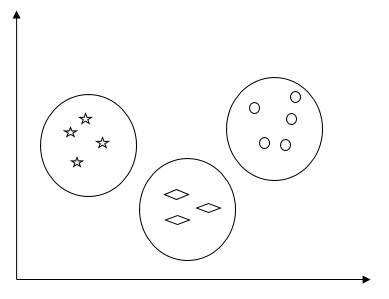
聚类数据的算法

以下是一些常见的聚类算法：

K-Means算法

K-means聚类算法是一个众所周知的聚类数据的方法。我们需要假设簇的数量已经知道。这也被称为平面聚类。它是一个迭代的聚类算法。下面列出的是该算法所需的步骤：

指定所需数量的K个子组。
固定簇的数量，并随机地将每个数据点分配到一个簇中。或者换句话说，我们需要根据簇的数量对数据进行分类。
在这一步骤中，应计算簇中心。
由于这是一个迭代算法，我们需要更新K个中心的位置，直到我们找到全局最优解，或者换句话说，中心点到达其最佳位置为止。

下面的代码将帮助在Python中实现K-means聚类算法。我们将使用Scikit-learn模块。

首先，导入必要的包：

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

接下来的代码行将通过使用sklearn.datasets包中的make_blobs来生成一个二维数据集，包含四个团块。

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples=500, centers=4,
                       cluster_std=0.40, random_state=0)

我们可以使用以下代码可视化数据集：

plt.scatter(X[:, 0], X[:, 1], s=50);
plt.show()

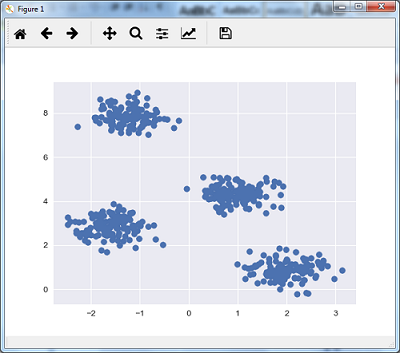
K 均值算法

初始化kmeans为KMeans算法，并设置参数为需要多少个簇(n_clusters)。

kmeans = KMeans(n_clusters=4)

训练K-means模型：

kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')

centers = kmeans.cluster_centers_

下面的代码将帮助我们绘制并可视化机器根据我们的数据以及根据要找到的簇的数量所做的发现：

plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5);
plt.show()

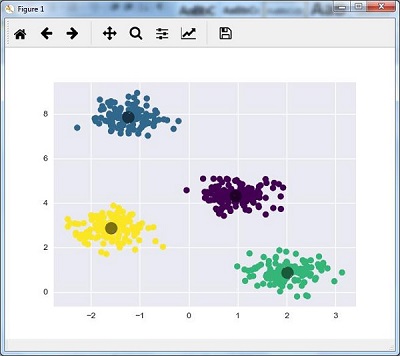
均值漂移算法

这是另一种流行的强大的无监督学习聚类算法。它不作任何假设，所以它是一个非参数化算法。它也被称为层次聚类或均值漂移聚类分析。以下是该算法的基本步骤：

首先，从数据点各自属于一个簇开始。

然后，计算质心，并更新新质心的位置。

重复这一过程，使我们更接近簇的峰值，即向更高密度的区域移动。

该算法在质心不再移动时停止。

下面的代码将帮助我们在Python中实现均值漂移聚类算法。我们将使用Scikit-learn模块。

首先，导入必要的包：

import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")

下面的代码将帮助生成一个二维数据集，包含四个团块，通过使用sklearn.datasets包中的make_blobs。

from sklearn.datasets.samples_generator import make_blobs

centers = [[2,2],[4,5],[3,10]]
X, _ = make_blobs(n_samples=500, centers=centers, cluster_std=1)
plt.scatter(X[:,0],X[:,1])
plt.show()

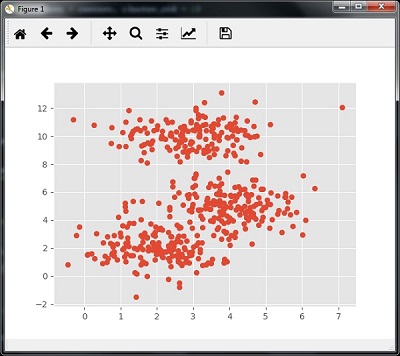
均值偏移算法

训练均值漂移聚类模型：

ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_

下面的代码将打印出簇中心以及根据输入数据预期的簇的数量：

print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)

下面的代码将帮助绘制并可视化机器根据我们的数据以及根据要找到的簇的数量所做的发现：

colors = 10*['r.','g.','b.','c.','k.','y.','m.']

for i in range(len(X)):
    plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize=10)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
            marker="x",color='k', s=150, linewidths=5, zorder=10)
plt.show()

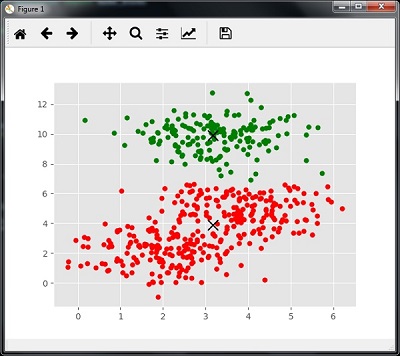
测量聚类性能

真实世界的数据并不是自然地组织成若干独特的簇。正因为如此，不容易可视化和得出结论。这就是为什么我们需要测量聚类性能及其质量。这可以通过轮廓分析来实现。

轮廓分析

这种方法可用于通过测量簇之间的距离来检查聚类的质量。基本上，它提供了一种评估参数的方法，例如通过给出轮廓分数来评估簇的数量。这个分数是一个度量标准，衡量每个簇中的点与邻近簇中的点的距离有多近。

轮廓得分分析

得分范围为[-1, 1]。以下是对此得分的分析：

得分为+1：接近+1的得分表明样本远离相邻的簇。
得分为0：得分为0表明样本位于或非常接近两个相邻簇之间的决策边界。
得分为-1：负得分表明样本已被错误地分配到了簇。

计算轮廓得分

本节将介绍如何计算轮廓得分。

轮廓得分可以通过以下公式计算：

$\text{silhouette score} = \frac{(p - q)}{\max(p, q)} \\$

其中，(p) 是数据点与其不属于的最近簇中所有点的平均距离，而 (q) 是数据点与其自身簇内所有点的平均距离。

为了寻找最优的簇数量，我们需要再次运行聚类算法，并从sklearn包中导入metrics模块。在下面的例子中，我们将运行K-means聚类算法来寻找最优的簇数量：

导入必要的包：

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

通过使用sklearn.datasets包中的make_blobs来生成一个二维数据集，包含四个团块：

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples=500, centers=4, cluster_std=0.40, random_state=0)

初始化变量：

scores = []
values = np.arange(2, 10)

遍历所有值并训练K-means模型：

for num_clusters in values:
    kmeans = KMeans(init='k-means++', n_clusters=num_clusters, n_init=10)
    kmeans.fit(X)
    
    # 使用欧几里得距离度量估计当前聚类模型的轮廓得分
    score = metrics.silhouette_score(X, kmeans.labels_, metric='euclidean', sample_size=len(X))
    
    # 显示簇的数量以及轮廓得分
    print("\nNumber of clusters =", num_clusters)
    print("Silhouette score =", score)
    
    scores.append(score)

找到最优簇数量：

num_clusters = np.argmax(scores) + values[0]
print('\nOptimal number of clusters =', num_clusters)

寻找最近邻

如果我们想要构建推荐系统，如电影推荐系统，那么我们需要理解寻找最近邻的概念。这是因为推荐系统利用了最近邻的概念。

寻找最近邻的概念可以定义为在给定数据集中找到最接近输入点的那个点的过程。K-最近邻(KNN)算法的主要用途是建立分类系统，这些系统根据输入数据点到各个类别的接近程度来对数据点进行分类。

下面的Python代码有助于找到给定数据集中K-最近邻：

导入必要的包，如下所示。在这里，我们使用sklearn包中的NearestNeighbors模块。

寻找最近邻

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import NearestNeighbors

# 定义输入数据
A = np.array([[3.1, 2.3], [2.3, 4.2], [3.9, 3.5], [3.7, 6.4], [4.8, 1.9],
              [8.3, 3.1], [5.2, 7.5], [4.8, 4.7], [3.5, 5.1], [4.4, 2.9]])

# 定义最近邻居数
k = 3

# 给定测试数据
test_data = [3.3, 2.9]

# 可视化和绘制输入数据
plt.figure()
plt.title('输入数据')
plt.scatter(A[:,0], A[:,1], marker='o', s=100, color='black')

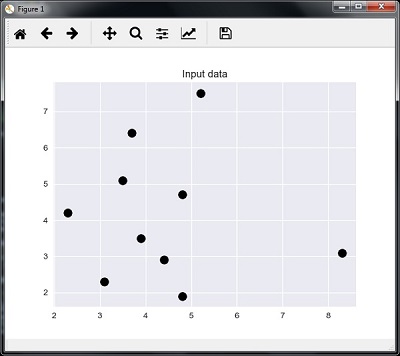
现在，我们需要构建K最近邻。对象也需要被训练：

knn_model = NearestNeighbors(n_neighbors=k, algorithm='auto').fit(A)
distances, indices = knn_model.kneighbors([test_data])

# 打印K最近邻
print("\nK 最近邻:")
for rank, index in enumerate(indices[0][:k], start=1):
    print(str(rank) + " 是", A[index])

# 可视化最近邻以及测试数据点
plt.figure()
plt.title('最近邻')
plt.scatter(A[:, 0], A[:, 1], marker='o', s=100, color='k')
plt.scatter(A[indices][0][:][:, 0], A[indices][0][:][:, 1],
           marker='o', s=250, color='k', facecolors='none')
plt.scatter(test_data[0], test_data[1],
           marker='x', s=100, color='k')
plt.show()

测试数据点

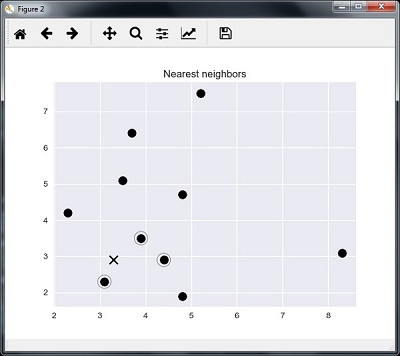
K 最近邻

1 是 [ 3.1 2.3]
2 是 [ 3.9 3.5]
3 是 [ 4.4 2.9]

K-最近邻分类器

K-最近邻（KNN）分类器是一种分类模型，它使用最近邻算法来分类一个给定的数据点。我们已经在上一节实现了KNN算法，现在我们将使用该算法来构建一个KNN分类器。

KNN分类器概念

K-最近邻分类的基本概念是找到预先定义的数量，即'k'——训练样本中最接近的新样本，该样本需要被分类。新的样本会从邻居本身获得标签。KNN分类器有一个固定的用户定义的常数来确定邻居的数量。对于距离，最常见的选择是标准欧氏距离。KNN分类器直接在已学习的样本上工作而不是创建学习规则。KNN算法是所有机器学习算法中最简单的之一。它在大量的分类和回归问题中已经取得了相当的成功，例如字符识别或图像分析。

示例

我们将构建一个KNN分类器来识别数字。为此，我们将使用MNIST数据集。我们将在Jupyter Notebook中编写此代码。

导入必要的包如下所示。这里我们使用sklearn.neighbors包中的KNeighborsClassifier模块：

from sklearn.datasets import *
import pandas as pd
%matplotlib inline
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import numpy as np

# 显示数字图像以验证要测试的图像
def Image_display(i):
    plt.imshow(digit['images'][i], cmap='Greys_r')
    plt.show()

# 加载MNIST数据集
digit = load_digits()
digit_d = pd.DataFrame(digit['data'][0:1600])

# 显示图像
Image_display(0)
Image_display(9)
# 获取数据集键
digit.keys()

# 创建训练和测试数据集，并将测试数据集供给KNN分类器
train_x = digit['data'][:1600]
train_y = digit['target'][:1600]
KNN = KNeighborsClassifier(20)
KNN.fit(train_x, train_y)

# 创建测试样本
test = np.array(digit['data'][1725])
test1 = test.reshape(1, -1)
Image_display(1725)
# 预测测试数据
KNN.predict(test1)

# 获取目标名称
digit['target_names']

输出：

array([6])

digit['target_names']

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])