回归是最重要的统计和机器学习工具之一。我们可以说机器学习的旅程始于回归。它可以被定义为一种参数技术,它允许我们基于数据做出决策,或者换句话说,它允许我们通过学习输入和输出变量之间的关系来基于数据做出预测。在这里,输出变量依赖于输入变量,并且是连续实数值。在回归中,输入和输出变量之间的关系很重要,它帮助我们理解随着输入变量的变化,输出变量的值如何变化。回归经常被用于价格预测、经济学、变化趋势等方面的研究。
在Python中构建回归模型
在本节中,我们将学习如何构建单变量以及多变量回归模型。
线性回归器/单变量回归器
首先,让我们导入一些所需的包:
import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt
现在,我们需要提供输入数据,并且我们已经将数据保存在一个名为linear.txt的文件中。
input = 'D:/ProgramData/linear.txt'
我们需要使用np.loadtxt函数加载此数据。
input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]
下一步是训练模型。我们将提供训练和测试样本。
training_samples = int(0.6 * len(X))
testing_samples = len(X) - training_samples
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]
现在,我们需要创建一个线性回归对象。
reg_linear = linear_model.LinearRegression()
使用训练样本训练对象。
reg_linear.fit(X_train, y_train)
我们需要用测试数据进行预测。
y_test_pred = reg_linear.predict(X_test)
现在绘制并可视化数据。
plt.scatter(X_test, y_test, color='red')
plt.plot(X_test, y_test_pred, color='black', linewidth=2)
plt.xticks(())
plt.yticks(())
plt.show()
输出
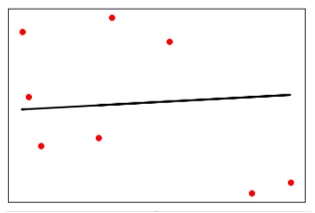
现在,我们可以计算线性回归的性能如下:
print("线性回归器的性能:")
print("平均绝对误差 =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("均方误差 =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("中位数绝对误差 =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("解释方差得分 =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2得分 =", round(sm.r2_score(y_test, y_test_pred), 2))
输出 线性回归器的性能:
平均绝对误差 = 1.78
均方误差 = 3.89
中位数绝对误差 = 2.01
解释方差得分 = -0.09
R2得分 = -0.09
在上面的代码中,我们使用了这个小数据集。如果你想使用更大的数据集,你可以使用sklearn.dataset来导入更大的数据集。
2,4.8
2.9,4.7
2.5,5
3.2,5.5
6,5
7.6,4
3.2,0.9
2.9,1.9
2.4,3.5
0.5,3.4
1,4
0.9,5.9
1.2,2.58
3.2,5.6
5.1,1.5
4.5,1.2
2.3,6.3
2.1,2.8
多变量回归器
首先,让我们导入一些所需的包:
import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
现在,我们需要提供输入数据,并且我们已经将数据保存在一个名为Mul_linear.txt的文件中。
input = 'D:/ProgramData/Mul_linear.txt'
我们将使用np.loadtxt函数加载此数据。
input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]
下一步是训练模型;我们将提供训练和测试样本。
training_samples = int(0.6 * len(X))
testing_samples = len(X) - training_samples
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]
现在,我们需要创建一个线性回归对象。
reg_linear_mul = linear_model.LinearRegression()
使用训练样本训练对象。
reg_linear_mul.fit(X_train, y_train)
现在,最后我们需要用测试数据进行预测。
y_test_pred = reg_linear_mul.predict(X_test)
打印回归器的性能:
print("线性回归器的性能:")
print("平均绝对误差 =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("均方误差 =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("中位数绝对误差 =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("解释方差得分 =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2得分 =", round(sm.r2_score(y_test, y_test_pred), 2))
输出 线性回归器的性能:
平均绝对误差 = 0.6
均方误差 = 0.65
中位数绝对误差 = 0.41
解释方差得分 = 0.34
R2得分 = 0.33
现在,我们将创建一个10阶的多项式并训练回归器。我们将提供样本数据点。
polynomial = PolynomialFeatures(degree=10)
X_train_transformed = polynomial.fit_transform(X_train)
datapoint = [[2.23, 1.35, 1.12]]
poly_datapoint = polynomial.fit_transform(datapoint)
poly_linear_model = linear_model.LinearRegression()
poly_linear_model.fit(X_train_transformed, y_train)
print("\n线性回归:\n", reg_linear_mul.predict(datapoint))
print("\n多项式回归:\n", poly_linear_model.predict(poly_datapoint))
输出 线性回归:
[2.40170462]
多项式回归:
[1.8697225]
在上面的代码中,我们使用了这个小数据集。如果你想使用更大的数据集,你可以使用sklearn.dataset来导入更大的数据集。
2,4.8,1.2,3.2
2.9,4.7,1.5,3.6
2.5,5,2.8,2
3.2,5.5,3.5,2.1
6,5,2,3.2
7.6,4,1.2,3.2
3.2,0.9,2.3,1.4
2.9,1.9,2.3,1.2
2.4,3.5,2.8,3.6
0.5,3.4,1.8,2.9
1,4,3,2.5
0.9,5.9,5.6,0.8
1.2,2.58,3.45,1.23
3.2,5.6,2,3.2
5.1,1.5,1.2,1.3
4.5,1.2,4.1,2.3
2.3,6.3,2.5,3.2
2.1,2.8,1.2,3.6